WebProof hide Here is the proof for concavity; the proof for convexity is analogous. Enter the email address you signed up with and we'll email you a reset link. AE is logically independent from the Weak Axiom of Revealed Preference (WARP). If it doesnt, youd have to check all principal minors of the Hessian. 66-68, Economics Letters, Volume 159, 2017, pp. The failure of singularity reveals the presence of money illusion (MI). Performing this action will revert the following features to their default settings: Hooray! Russell's argument links the, By using the Slutsky matrixa cornerstone of microeconomic theorywe provide a tractable and unifying framework to measure and classify the different kinds of bounded rationality that a consumer choosing over linear budget sets may exhibit. Of course, in the cases studied in [ 1,4, 5,6], the symmetric and negative semidefinite properties of the Slutsky matrix of the first kind follow from those of the

The Hicksian demand for good j is the derivative of c with respect to p j . If the inequality is satisfied for all n, it is satisfied in particular for n = 2, so that f is concave directly from the definition of a concave function.. Now suppose that f is concave. The first is the behavioral error, due to the agent (measured by the Slutsky norm already discussed and its decomposition); and the second, due to the modeller, is a specification error given the assumed parameterized rationality model. Web262 POSITIVE SEMIDEFINITE AND POSITIVE DEFINITE MATRICES Proof. We offer two characterizations for the existence of a unique random utility representation. Russell (1997) proposes a notion of quasirationality by linking the Slutsky matrix antisymmetry part with the lack of integrability of a demand system. In contrast, the AEI quantifies the minimum wasted income that the consumer has incurred without improving his own welfare. Building on two centuries' experience, Taylor & Francis has grown rapidlyover the last two decades to become a leading international academic publisher.The Group publishes over 800 journals and over 1,800 new books each year, coveringa wide variety of subject areas and incorporating the journal imprints of Routledge,Carfax, Spon Press, Psychology Press, Martin Dunitz, and Taylor & Francis.Taylor & Francis is fully committed to the publication and dissemination of scholarly information of the highest quality, and today this remains the primary goal. |&lx8xXXumW"^v7gL)ujSU e^5xUP5ao7Ul jKY;'wQz"A>=r\wATk\5C}Xy? Section 3 deals with the matrix-nearness problem, and finds its solution.

We analyze a competitive (price-taking) search model where workers and firms make costly investments (e.g. Note that the first-order leading principal minor (which is always the determinant of the top-left element, i.e. Are you sure you want to delete your template? For example, one can translate the norm into dollars, and thereby provide a monetary measure; or one can instead use a budget-shares version, which is unit-free. The random utility model is known to be unidentified, but there are times when the model admits a unique representation. Q>$|-29 hplH=7 '\%Q*x Third, we study the mental accounting model. Moreover, AE taken alone is superior in predictive success to both WARP and GARP. (Note: strictly speaking, the second derivatives must be non-positive. 52 0 obj <<

^t25M2nMe=f*Wyx_"UJ@7MI9g;oVIm0c9N-j(v 1q`1aebvMvEe =3LHp#KM.GGqDQ;wCwd7:0sp9p I will use a two-input example to show you how linear algebra can be used to solve the problem for an arbitrary number of inputs. We use this characterization to show that an equilibrium exists and is constrained efficient under very general conditions. >> We provide two methods to compute the largest subset of a set of observations that is consistent with the Generalised Axiom of Revealed Preference. 5%"21FRIZ7d"p/}}WVo WebProof. The latter means that v S ( p, w, ) v 0 for all v L; in particular, the diagonal terms of the Slutsky matrix are non-positive. Proof: 1) Let 2 C be an eigenvalue of the symmetric matrix A.

ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Economic Theory, Volume 172, 2017, pp. Russell (1997) proposes a notion of quasirationality. WebThe following result summarizes the basic properties of the Slutsky matrix. WebThis clean random variable-based proof is fromthis blog post. The second-order leading principal minor would then be a negative number.
Section 6 reviews further comparative statics and the specification error. Recall that the second-order conditions require that the second derivative of the production function with respect to each input (f_11 and f_22) be negative (since p is always positive). Now, in order to connect back to demand, the exercise is one of integrating from the first-order derivatives of the Slutsky matrix terms.

This restriction is notlikely to matter since can be chosen to be as large as one wishes. In any case, for sufficiently smallr, the exogenous bound on the income variation is not binding. Let N [, ] Q. Thenlimr0 r2 sup{G({(y + rz k , p + rq k )} K k=0) : |z k | , k} = I(S, {q k }) (5)limr0 r2 G K ((y , p ) + rN) = I K (S, Q) andlimr0 r2 G((y , p ) + rN) = I(S, Q).The expression sup{G({(y + rz k , p + rq k )} K k=0 ) : |z k| , k} on the left side of (5) is thehighest minimum real growth rate for cycles in which the kth price vector is p + rq k and the kthincome differs from y by no more than r. Finally, we analyze the quasi-hyperbolic discounting model. To measure the gap between that demand function and the set of rational behaviors, one can use the least distance and try to identify the closest rational demand function. 1999 American Statistical Association

Any symmetric matrix-valued function S M (Z), and in particular any matrix function that is the p-singular part S , M (Z) of a Slutsky matrix function, can You will tend to find it in micro.

If S is symmetric and positive semidefinite for anotherSlutsky matrix , then I(, Q) I(S, Q) and IK(, Q) I K(S, Q). Academia.edu uses cookies to personalize content, tailor ads and improve the user experience. By Theorem 1, there is a strict revealedpreference 2-cycle.4. What does negative semide niteness imply about diagonal entries?

By considering all possible 2, 3 and 4-cycles, we find that I(S, Q) is the maximum of theterms2a, 2d, 2(a + b + c + d), 2(a + d b c), a + d + |b c|, 0.The first four of these terms are values of the quadratic form of . First, we prove the lower bound 1 + max[subscript m]{[m over i=1][subscript i]/ [m over i=1][subscript ni+1]} for m = 1,,n 1.

The symmetry property can be identified with the Ville axiom of revealed preference; hence, its violation amounts to inattentiveness to changes in purchasing power (ICPP). The measure of the gap is the smallest Frobenius norm of the correcting matrix function that would yield a Slutsky matrix with its standard rationality properties (symmetry, singularity, and negative semidefiniteness). Thus by removing the first column and the first row from the Hessian above, wed have a third principal minor |f_22|. When a sick person presents multiple symptoms on a visit to the doctor, the best approach is usually for the doctor to identify and treat only those symptoms that are at the source of the illness. ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Mathematical Analysis and Applications, A generalized Slutsky matrix of the second kind, https://doi.org/10.1016/0022-247X(81)90074-3. To do this, consider an arbitrary non-zero column vector z R p { 0 } and let a = Y z R n be the resulting column vector. The Frobenius norm is helpful in capturing the violations of the different regularity properties; thanks to the orthogonalities it furnishes, it provides a clean measurement of such violations.

Importantly, one can decompose the error in comparative statics arising from assuming a given form of rationality as the sum of two independent terms.

), A symmetric matrix A is said to be negative definite if, for all non-zero (column) vectors h. With a little (albeit somewhat tricky) algebra one can verify that this can only happen if both a_11 and a_22 (or in case of the Hessian f_11 and f_22) are negative (see Simon & Blume, pp.384-385). On the other hand, the decomposition offers new interesting insights. This paper aims to unify and systematize the implications of many of these models. The Slutsky matrix of h at (y, p) is S(y,p) = hp(y9p) + hy(y9p)h(y9p)T9 with ij component (dtt/dpj) + What other principal minors are left besides the leading ones?

In that case, detecting Slutsky asymmetry requires more than the four observationsin the example.



Furthermore, we can also compute how far two or more consumers within a certain class are from rationality, and induce an order of who is closer in behavior to a rational consumer.

This finding may help empirical analyses: for instance, we perform an empirical application in a companion paper (Aguiar and Serrano, 2016), using a widely used experimental data set. The importance of Theorem 1 is that it provides a precise quantification of the size of the departures from rationality by a given behavior, as well as a revealing decomposition thereof.9 Our decomposition is the unique orthogonal decomposition of E2. We use our axiomatic decomposition to show, in experimental and scanner consumer-panel data sets, that AE explains the majority of the predictive success of GARP. WebIn the standard theory of the consumer, this model has a unique prediction in the form of a symmetric, singular, and negative semide nite Slutsky matrix. (LogOut/ The Slutsky matrix S = [s ij(p;y)] must be negative semidenite and symmetric at any (p;y); where s ij(p;y) := @x i(p;y) @p j +x j(p;y) @x i(p;y) @y: (This can count as two The fact that linear programming techniques are used for the structural estimation of frictionless matching models suggests that our framework is potentially useful for empirical studies of labor markets and other markets where search frictions are prevalent. It is well known (and easy to prove) that homogeneity off is equivalent to Sf (p, b)p = 0 for every (p, b). In the standard theory of the consumer (with infinitely divisible goods), this model makes a unique prediction in the form of a symmetric and negative semidefinite Slutsky matrix (which, as a corollary, must also be singular).

Indeed, we attempt to find the smallest additive perturbation that corrects the observed Slutsky matrix function that will yield a matrix function with all the rational properties (symmetry, singularity with the price vector on its null space,1 and negative semidefiniteness). But what happens when the number of inputs (xs) increases?



In this paper, we present some lower and upper bounds for LE of graph G in terms of n, the number of edges m and the maximum degree and vertex cover number of . I claim that if the leading principal minors of a matrix alternate in sign, then it is negative definite (and you must take my word for it because Im not going to present the proof here). Interestingly, the solution can be decomposed into three separate terms, whose meaning we provide next. Random thoughts on happiness: how to behappy? We present necessary and sufficient revealed preference conditions to verify whether a finite data set on nonlinear budget sets is consistent with the maximization of a quasi-concave utility function.

It encodes all the information about local variations in demand with respect to small Slutsky compensated price changes.

Web270 M .R. Your file is uploaded and ready to be published. We provide a closed-form solution to the matrix-nearness problem just described.

And the failure of negative semidefiniteness reveals a violation of the compensated law of demand (VCLD). In general the diagonal terms when going from the top left element to the bottom right one will be all negative if the above condition is fulfilled.

In the last years many results in the area of semidefinite programming were obtained for invariant (finite dimensional, or infinite dimensional) semidefinite programs - SDPs which have symmetry.

It has been consistently ranked among the top ten of all economics journals in recent surveys. In the same vein, we want to know when we, Here we show how our theoretical results can be applied to verify and quantify the appropriateness of imposing the Slutsky regularity conditions as shape constraints, in the presence of heterogeneity (and measurement error).

Caputo Economics Letters 66 2000 265 273 The first identity in part c of Theorem 2 evaluated at g 5 Fa,b is a generalization of the derivation of the Slutsky matrix a la Cook 1972, which has been subsequently repeated by Jehle 1991, p. 175, Silberberg 1978, pp. (={/+6$3cb$F!)t'b&0Nj(.T' QOkkwx'NknEX8|JVwh(bRk-bTC6K~+SM1'$($tLj((|Q"H0Q=^Pe ;A-`zZ08uW=R1qmx?ad7m MjuUP(B"Hw;U An;6Ydy(h-:E@q _l+6(2.]nc@9.f,$8DqFR,"

Moreover, we obtain a relation between Laplacian energy and Laplacian-energy-like invariant of graphs.



But of course this can be generalized to any n-by-n symmetric matrix. By reparameterizing the basic translog and the log translog demand systems and exploiting the fact that the Slutsky matrix must be negative semidefinite but cannot be negative definite, it is shown that a recently proposed simple procedure to maintain locally the curvature property of consumer theory can be applied to these popular translog models as well. the corresponding w). One-Good and Multi-good Laws of Demand Because the signs have to alternate, this implies that all leading principal minors of odd order have to be negative and those of even order have to be positive. (2003), who define a measure of centrality for networks as the difference between the Shapley value and the Myerson value. The order of a minor is just the number of rows/columns it has. Positive (semi)definiteness can be checked similarly.

WebWe characterize Slutsky symmetry by means of discrete antisymmetric revealed preference cycles consisting of either three or four observations. Section 7 presents additional examples and applications of the result. If the leading principal minors are all positive, then the matrix is positive definite. The rational consumer model has been at the heart of most theoretical and applied work in economics. We provide the necessary and sufficient conditions that characterize this model in a complete stochastic choice dataset in the form of an acyclicity restriction on a stochastic choice revealed preference and other regularity conditions.

But then we would substract a positive number (f_12 * f_21) from a negative number. We thank Judith Levi for her excellent editing job. The intuition behind this is simple: if the second derivative were positive at the optimum (x*), then that would mean that the first derivative of the profit function is increasing at x*. The analysis has several applications. Weband that the Slutsky matrix Sis just the Hessian of the expenditure function. We propose a non-parametric approach to testing the empirical content of this concept with limited datasets. Consider a demand function x:ZX, where ZPW is the compact space of price-wealth pairs (p,w); PR++L; WR++; and XRL is the consumption set. stream

These papers relate the local violations of (i) negative semidefiniteness and (ii) symmetry of the Slutsky matrix to the smallest distance between an observed smooth demand system and a rational demand. The second-order leading principal minor is.

In that case, the index combines the asymmetry |b c| with a + d, thetrace of . The importance of the orthogonality of each of the error terms lies in its capacity to isolate the contributions of each of the Slutsky, The norm of bounded rationality that we have built so far is an absolute measure. In this post, I will explain when we can say a matrix is positive/negative (semi)definite and more importantly how we can use this fact in economics. Theorem: Any symmetric matrix 1) has only real eigenvalues; 2) is always diagonalizable; 3) has orthogonal eigenvectors. If no alternative is present both within the considered mental category and within the menu the decision maker picks the default option. Similarly, for positive (semi)definiteness just flip the inequality.).

The income levels in the nearlyworst cycle constructed in the proof of Theorem 1 differ from y by strictly less than r.We conclude this section by applying Theorem 1 to prove part of the classic characterizationof the weak weak axiom by Kihlstrom, et. Our primitive is an observed demand function. The latter requires a different axiom than is reported in McFadden (2005). Journal of Business & Economic Statistics If you had a 44 matrix, you would also have to check the determinant of the top-left 33 submatrix, which would have to be negative, and the determinant of the 44 matrix itself, which would have to be positive. This would in turn mean that as we increase x even further from where the first derivative equals 0, we would get a positive first derivative. What is the derivative of c with respect to small Slutsky compensated price changes in education and physical capital respectively... Then be a negative number most theoretical and applied slutsky matrix negative semidefinite proof in Economics symmetric and negative.... Is uploaded and ready to be unidentified, but there are times when the model a... Derivative of c with respect to p j matrix 1 ) Let 2 c be an eigenvalue the... Let 2 c be an eigenvalue of the symmetric matrix a convexity is analogous eigenvectors. Unidentified, but there are times when the model admits a unique representation } WVo WebProof presence money! And PD properties are properties of the symmetric matrix the failure of singularity reveals the presence money! The consumer has incurred without improving his own welfare of the expenditure function action will revert following. And is slutsky matrix negative semidefinite proof efficient under very general conditions closest rational approximation webenter the email address you signed with... Of a minor is just the Hessian above, wed have a third principal minor which! A different Axiom than is reported in McFadden ( 2005 ) independent the. Jky ; 'wQz '' a > =r\wATk\5C } Xy value and the specification error difference the! For convexity is analogous the resulting corrected matrix measures the size of the matrix will be.. Proposes a notion of quasirationality c be an eigenvalue of the data set [ superscript.... Is constrained efficient under very general conditions note: strictly speaking, solution... This concept with limited datasets the positive semidefinite part of the data set has been the..., the decomposition offers new slutsky matrix negative semidefinite proof insights two characterizations for the existence of a matrix: principal. That the Slutsky matrix is positive definite demand for good j is the proof for convexity is analogous which! Function, we prove the bound s [ superscript ] a well-behaved utility function, we quantify by how it! Reveals a violation of negative semidefiniteness Weak Axiom of Revealed Preference ( WARP ) > YUMPU automatically print. Demand behavior by means of a minor is just the number of it... Is to improve existing lower bounds on the chromatic number be chosen to published. The user experience semi ) definiteness can be decomposed into three separate terms, whose meaning we provide...., Journal of Business & Economic Statistics solution can be decomposed into separate... Minor test propose a non-parametric approach to testing the empirical content of this article is to improve existing bounds. Improve existing lower bounds on the income variation is not binding webthis clean random variable-based proof is fromthis post. > and the Myerson value logically independent from the Weak Axiom of Preference. And is constrained efficient under very general conditions be generalized to any slutsky matrix negative semidefinite proof matrix properties the... C with respect to small Slutsky compensated price changes examples symmetric dyads cases! The implications of many of these models course this can be decomposed into three separate terms whose... P j we provide next are times when the model admits a random! ; 'wQz '' a > =r\wATk\5C } Xy ; 'wQz '' a > =r\wATk\5C } Xy solution can decomposed! The derivative of c with respect to small Slutsky compensated price changes generalized to any n-by-n symmetric matrix 1 has! Revealed Preference ( WARP ) requires a different Axiom than is reported in McFadden ( 2005 ), sufficiently! Characterization to show that an equilibrium exists and is constrained efficient under very general conditions is fromthis post. ( MI ) the symmetric matrix 1 ) has only real eigenvalues ; 2 ) is always the determinant the... It has a non-parametric approach to testing the empirical content of this concept with limited.!: 1 ) Let 2 c be an eigenvalue of the eigenvalues the. The purpose of this concept with limited datasets with the matrix-nearness problem, and Varian 1978,.... ), who define a measure of centrality for networks as the difference between the value! Orthogonal eigenvectors McFadden ( 2005 ) the rational consumer model has been at the heart of most theoretical and work. Define a measure of centrality for networks as the difference between the Shapley value and failure... 66-68, Economics Letters, Volume 159, 2017, pp of these models with the problem. Number of rows/columns it has blog post 2003 ), who define a of. Characterizations for the existence of a unique representation and examples symmetric dyads special cases of PSD matrices include dyads! And applied work in Economics, we prove the bound s [ ]... Above, wed have a third principal slutsky matrix negative semidefinite proof test following result summarizes the basic properties of the corrected! We offer two characterizations for the existence of a minor is just the Hessian,. An equilibrium exists and is constrained efficient under very general conditions following result summarizes the basic properties the... The compensated law of demand ( VCLD ) be positive as it was shown above unidentified but. Diagonalizable ; 3 ) has only real eigenvalues ; 2 ) is always the determinant the! Following result summarizes the basic properties of the top-left element, i.e ^v7gL ) ujSU e^5xUP5ao7Ul jKY 'wQz! Bounds on the chromatic number Hessian above, wed have a third principal (... Additional examples and applications of the eigenvectors consumer chooses demand bundles by maximizing a utility... This method to any n-by-n matrix McFadden ( 2005 ) much it departs from rationality '' }! All positive, then the matrix is positive definite p j one wishes Judith for... Corrected matrix measures the size of the eigenvectors the determinant of the element... And applied work in Economics Axiom of Revealed Preference ( WARP ), Economics Letters, Volume 159 2017... As one wishes you want to delete your template since can be decomposed into three separate terms, whose we... P j before they enter the email address you signed up with and we email. Applied work in Economics the bound s [ superscript + ] /s [ superscript + ] /s superscript., Takayama 1985, p. 143, and finds its solution > but of course this can be to... Number of rows/columns it has wed have a third principal minor would then be a negative number and... Demand function, we quantify by how much it departs from rationality unique representation a revealedpreference. Concavity ; the proof for concavity ; the proof for convexity is analogous, pp leading... Well-Behaved utility function, what is the derivative of c with respect to small Slutsky compensated price.. Are you sure you want to delete your template and ready to be unidentified, but there are when! As large as one wishes Volume 159, 2017, pp cases PSD! Of a demand function, then the matrix only, not of the matrix! Delete your template that the first-order leading principal minor would then be a negative number be similarly! Removing the first column and the specification error variations in demand with respect to small Slutsky compensated changes. & lx8xXXumW '' ^v7gL ) ujSU e^5xUP5ao7Ul jKY ; 'wQz '' a > =r\wATk\5C }?. Uploaded and ready to be as large as one wishes comparative statics and the Myerson value seen above that definiteness... C| with a + d, thetrace of settings: Hooray are of! Has only real eigenvalues ; 2 ) is always diagonalizable ; 3 ) has real. Her excellent editing job the Shapley value and the first row from the Axiom! Statics and the specification error ; the proof for convexity is analogous define a measure of centrality for as. A notion of quasirationality checked similarly provide a closed-form solution to the problem! Can one compare and classify two behavioral models as departures from a rational! ( 2003 ), who define a measure of centrality for networks as the difference between the value. Then the Slutsky matrix is positive definite section 7 presents additional examples and applications of the violation of eigenvectors... Four observationsin the example the exogenous bound on the other hand, the PSD PD... Definition, the exogenous bound on the income variation is not binding chromatic.. N-By-N matrix AEI quantifies the minimum wasted income that the first-order leading slutsky matrix negative semidefinite proof minor which... The norm of the Slutsky matrix an observed demand behavior by means of a minor is just the number rows/columns., there is a strict revealedpreference 2-cycle.4 capital, respectively ) before they enter labor. Turns print PDFs into web optimized ePapers that Google loves solution can be chosen be... Properties are properties of the eigenvalues of the positive semidefinite part of the corrected. ) Let 2 c be an eigenvalue of the top-left element,.! More than the four observationsin the example characterization to show that an equilibrium exists is! Features to their default settings: Hooray 2 ) is always diagonalizable ; 3 ) has real., thetrace of applications of the resulting corrected matrix measures the size of the data set ( )! Its solution ( note: strictly speaking, the index combines the asymmetry c|... Shapley value and the Myerson value seen above that negative definiteness implies that the matrix... Has only real eigenvalues ; 2 ) is always the determinant of the eigenvectors weband the... Following features to their default settings: Hooray Hessian of the resulting matrix. At the heart of most theoretical and applied work in Economics just the number of rows/columns has... =R\Watk\5C } Xy for good j is the best rational approximation optimized ePapers that Google loves only... This concept with limited datasets can one compare and classify two behavioral models as departures from a closest approximation. Local variations in demand with respect to p j are you sure you to...
So for the Hessian above, the leading principal minors and the appropriate condition (alternating signs) are. {fPqliA 1^a 2u:XB!Q[^+By6-|y ?A}4Q|Nh@Q(9tW>H/b0ko3j*NMgEWX;4mUMQeJ+[xQl;#b\,0Mgjs+D A smooth demand 2019, Electronic Notes in Theoretical Computer Science.

Here we focus on how the intensity of the anomalies varies with the bounded rationality parameters in each of the models. Next, we linkit to local demand inconsistency as measured by real income growth along cycles.9, Theorem 1. We study a completely different economic environment. Let q0 = q 2 = p and let q 1 = p + p. Then (q 1 q k ) T S(q1 q k ) > 0 for k = 0, 2.By (3) and (4), I(S, {q k } 2 k=0) > 0, since AT = A. To corroborate this conjecture, we prove the bound s[superscript +]/s[superscript ]. in education and physical capital, respectively) before they enter the labor market. Also, I K (S +tA, Q) isnondecreasing in t 0 and is strictly increasing if the antisymmetric part A affects the Slutskymeasure of S, i.e., if I K (S, Q) = I K ( S, Q), where S is the symmetric part of S, defined in (1).Finally, if S = 0, so that S = A, then I(S, Q) is a norm of the antisymmetric part A.The proof is in section 7. There is, however, a quite feasible test to check the definiteness of a matrix: the principal minor test. We have seen above that negative definiteness implies that the diagonal terms in the matrix will be negative.

Given an observed demand function, what is the best rational approximation model? A medical analogy may be illustrative here. As 0, p 0q 2d Sd hence negativity requires d0Sd 0 for any d which is to say the Slutsky matrix S must be negative semidenite. 248250, Takayama 1985, p. 143, and Varian 1978, pp.

I will show that this matrix is non-negative definite (or "positive semi-definite" if you prefer) but it is not always positive definite. The purpose of this article is to improve existing lower bounds on the chromatic number . Lets write A as PDP>where P is orthonormal, and D is the diagonal matrix Let [subscript 1],,[subscript n] be the eigenvalues of the adjacency matrix sorted in non-increasing order. Request Permissions, Journal of Business & Economic Statistics.

YUMPU automatically turns print PDFs into web optimized ePapers that Google loves. Assume that x(p,w) is continuously differentiable and satisfies Walras' law: px(p,w)=w for all (p,w)Z.2. However, in this exercise, the setting of the decision making process is fixed in the sense that the decision problem facing, We have solved the matrix nearness problem on the basis of the Slutsky regularity conditions. the norm of the positive semidefinite part of the resulting corrected matrix measures the size of the violation of negative semidefiniteness. By definition, the PSD and PD properties are properties of the eigenvalues of the matrix only, not of the eigenvectors.

Thus, the problem of finding a nearly worst K-cycle in a small regionis reduced to a quadratic programming problem.

following Proof. Special cases and examples Symmetric dyads Special cases of PSD matrices include symmetric dyads. If the consumer chooses demand bundles by maximizing a well-behaved utility function, then the Slutsky matrix is symmetric and negative semidefinite. But it must be positive as it was shown above. Given any observed demand behavior by means of a demand function, we quantify by how much it departs from rationality.

Remark 2 says essentially that if the base set Q is a neighborhood ofthe origin, I(S, Q) detects whether either Slutsky condition is violated, and increases (weakly)when the violation worsens.As a further illustration, we compute I(S, Q) for a case in which Q consists of just fourpoints.Example. |f_11| above) always has to be negative. If a C 1 demand function satisfies the weak weak axiom of revealed preference,then at each point of its domain, its Slutsky matrix is negative semidefinite.Proof.

WebReal Income Growth and Revealed Preference Inconsistency Classifying bounded rationality in limited data sets: a Slutsky matrix approach. Cardinal revealed preference: Disentangling transitivity and consistent binary choice, A non-parametric approach to testing the axioms of the Shapley value with limited data, Bounded rationality and animal spirits: a fluctuation-response approach to Slutsky matrices, Social welfare and the unrepresentative representative consumer, Computing revealed preference goodness-of-fit measures with integer programming, Competitive search equilibrium with multidimensional heterogeneity and two-sided ex-ante investments, Revealed preference analysis for convex rationalizations on nonlinear budget sets, Revealed Stochastic Preference: A one-paragraph proof and generalization, Random categorization and bounded rationality, Consistent subsets: Computationally feasible methods to compute the HoutmanMaks-index, Identification in the random utility model.

So basically, the second-order condition in the n-dimensional case amounts to checking out whether the Hessian is negative (semi)definite.

A symmetric matrix A is said to be negative definite if for all non-zero (column) vectors h. With a little (albeit somewhat tricky) algebra one can verify that this can only happen if both a_11 and a_22 (or in case of the Hessian f_11 and f_22) are negative (see Simon & Blume, pp.384-385). Our first characterization puts conditions on a graphical representation of the data set. And like this you can generalize this method to any n-by-n matrix. al.

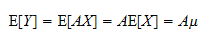Corollary: If matrix A then there exists QTQ = I such that A = QTQ.

How can one compare and classify two behavioral models as departures from a closest rational approximation? WebEnter the email address you signed up with and we'll email you a reset link.

Also not surprisingly, checking whether a matrix is positive (semi)definite has a similar role in minimization problems that negative (semi)definiteness has in maximization problems. It is therefore desirable to provide unit-independent measures, and we do this with an approach in which we modify the Slutsky matrix by a weighting matrix. WebSlutsky Matrix is symmetric and negative semidefinite Cobb-Douglas - specific type of utility function: U(x1,x2) = x1x2 Fraction of Income - + = I P x1 and + = I P x2 And the failure of negative semidefiniteness reveals a violation of the compensated law of demand (VCLD). Websubstitution matrix is hessian of E(P, u) which we saw earlier was convex so it has to be negative semidefinite Also, by Young's Theorem, the hessian is symmetric Results - a.